Evaluates trigonometric and hyperbolic values.
Accepts one argument X as input and returns the sine of X.
Syntax:
| process eval("identifier=sin(X)")
Example:
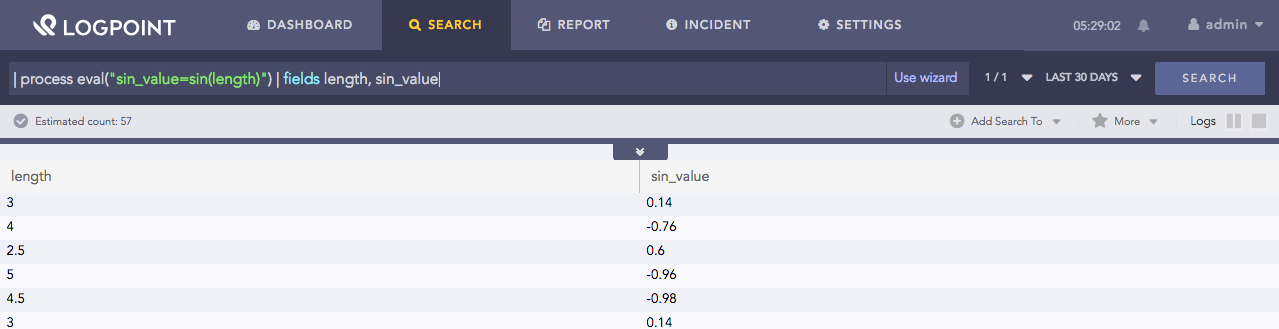
| process eval("sin_value=sin(length)") | fields length, sin_value
Using sin function¶
Here, the query returns the sine of the length field in the sin_value identifier.
The fields command displays the value of length and sin_value fields in a tabular form.
Accepts one argument X as input and returns the hyperbolic sine of X.
Syntax:
| process eval("identifier=sinh(X)")
Example:
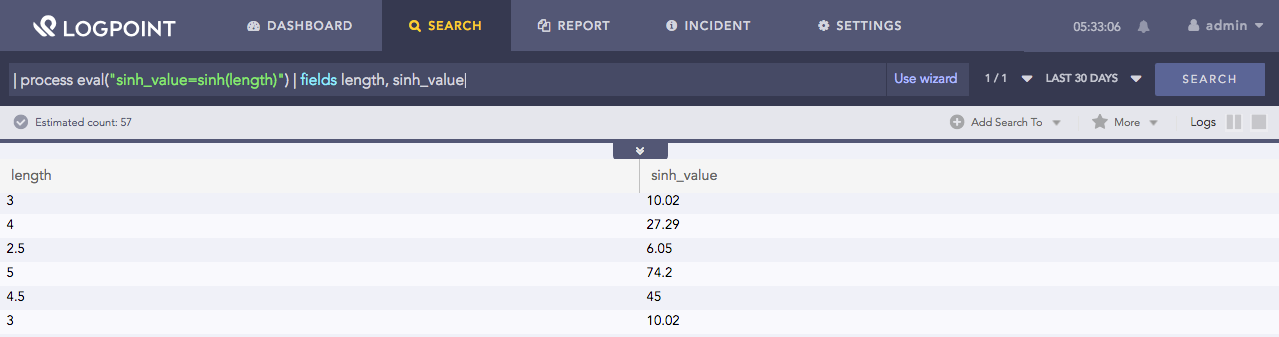
| process eval("sinh_value=sinh(length)") | fields length, sinh_value
Using sinh function¶
Here, the query returns the hyperbolic sine of the length field in the sinh_value identifier.
Accepts one argument X as input and returns the inverse sine of X. The value of X must be in the range from -1 to 1 inclusive.
Syntax:
| process eval("identifier=asin(X)")
Example:
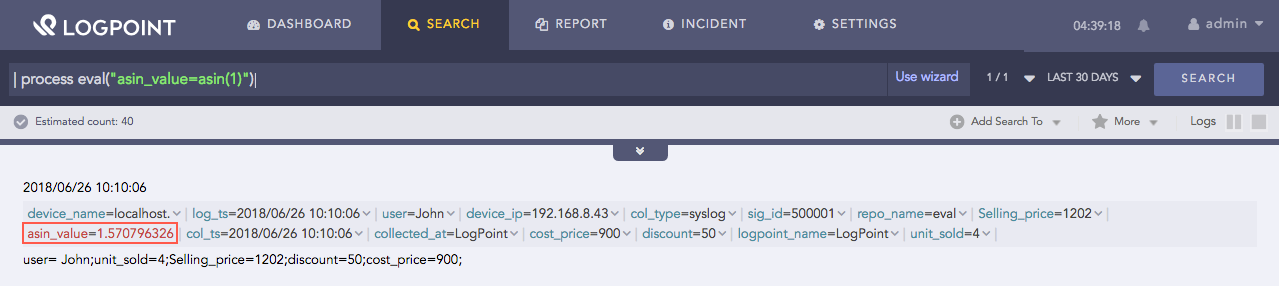
| process eval("asin_value=asin(1)")
Using asin function¶
Here, the query returns the inverse sine of 1 in the asin_value identifier.
Accepts one argument X as input and returns the inverse hyperbolic sine of X.
Syntax:
| process eval("identifier=asinh(X)")
Example:
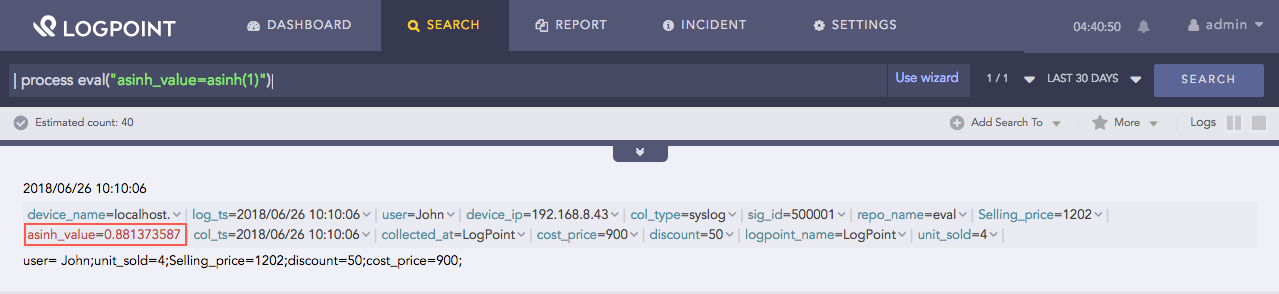
| process eval("asinh_value=asinh(1)")
Using asinh function¶
Here, the query returns the inverse hyperbolic sine of 1 in the asinh_value identifier.
Accepts one argument X as input and returns the cosine of X.
Syntax:
| process eval("identifier=cos(X)")
Example:
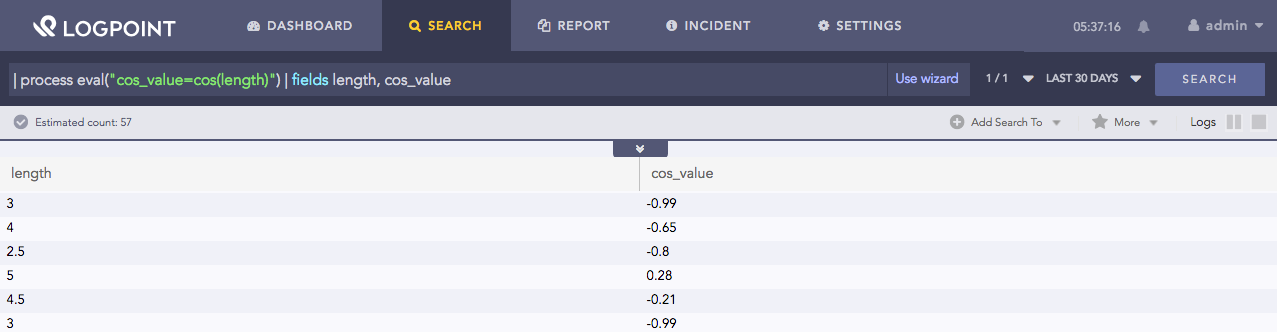
| process eval("cos_value=cos(length)") | fields length, cos_value
Using cos function¶
Here, the query returns the cosine of the length field in the cos_value identifier.
The fields command displays the value of length and cos_value fields in a tabular form.
Accepts one argument X as input and returns the hyperbolic cosine of X.
Syntax:
| process eval("identifier=cosh(X)")
Example:
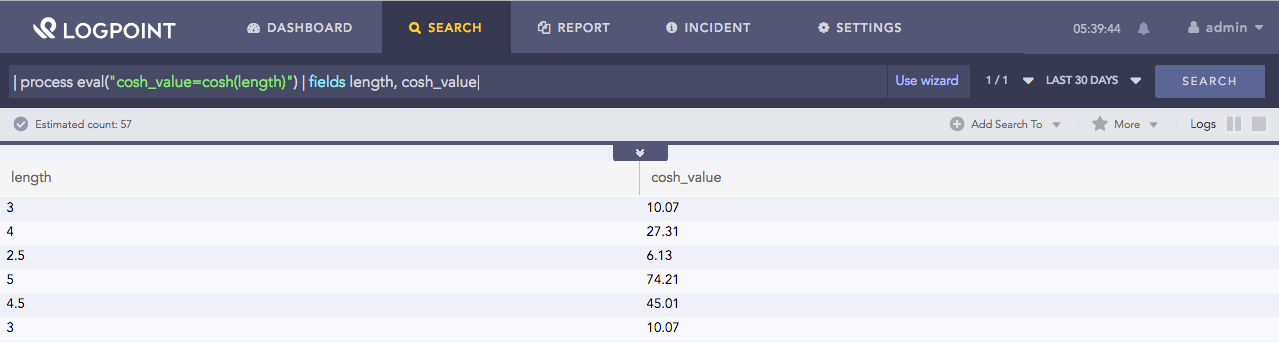
| process eval("cosh_value=cosh(length)") | fields length, cosh_value
Using cosh function¶
Here, the query returns the hyperbolic cosine of the length field in the cosh_value identifier.
The fields command displays the value of length and cosh_value fields in a tabular form.
Accepts one argument X as input and returns the inverse cosine of X. X must be in the range from -1 to 1 inclusive.
Syntax:
| process eval("identifier=acos(X)")
Example:
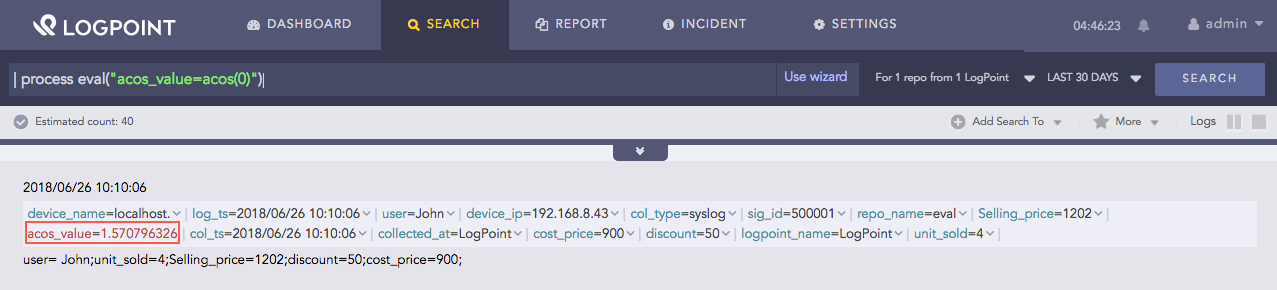
| process eval("acos_value=acos(0)")
Using acos function¶
Here, the query returns the inverse cosine of 0 in the acos_value identifier.
Accepts one argument X as input and returns the inverse hyperbolic cosine of X.
Syntax:
| process eval("identifier=acosh(X)")
Example:
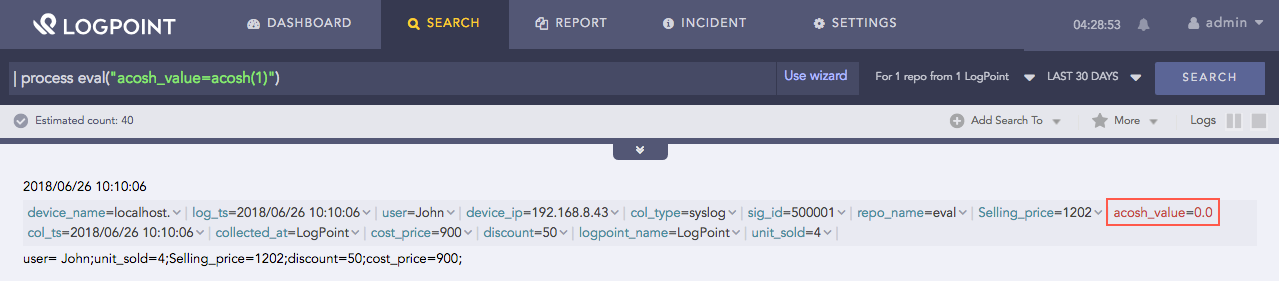
| process eval("acosh_value=acosh(1)")
Using acosh function¶
Here, the query returns the inverse hyperbolic cosine of 1 in the acosh_value identifier.
Accepts one argument X as input and returns the tangent of X.
Syntax:
| process eval("identifier=tan(X)")
Example:
| process eval("tan_value=tan(length)")
| fields length, tan_value
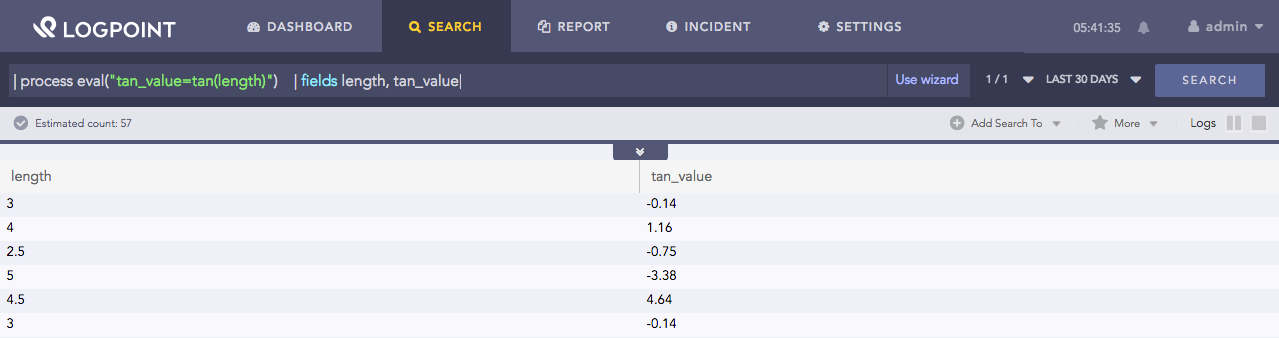
Using tan function¶
Here, the query returns the tangent of the length field in the vtan_value identifier.
The fields command displays the value of length and tan_value fields in a tabular form.
Accepts one argument X as input and returns the hyperbolic tangent of X.
Syntax:
| process eval("identifier=tanh(X)")
Example:
| process eval("tanh_value=tanh(length)")
| fields length, tanh_value
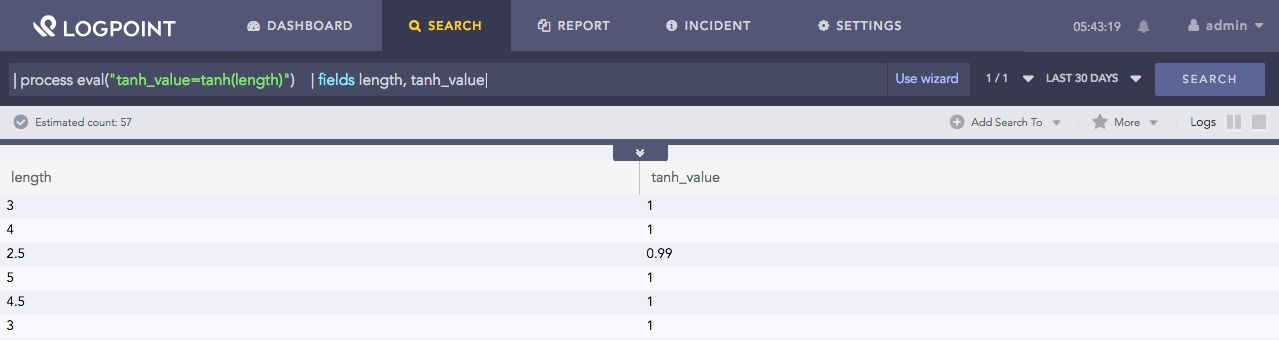
Using tanh function¶
Here, the query returns the hyperbolic tangent of the length field in the tanh_value identifier.
The fields command displays the value of length and tanh_value fields in a tabular form.
Accepts one argument X as input and returns the inverse tangent of X.
Syntax:
| process eval("identifier=atan(X)")
Example:
| process eval("atan_value=atan(1)")
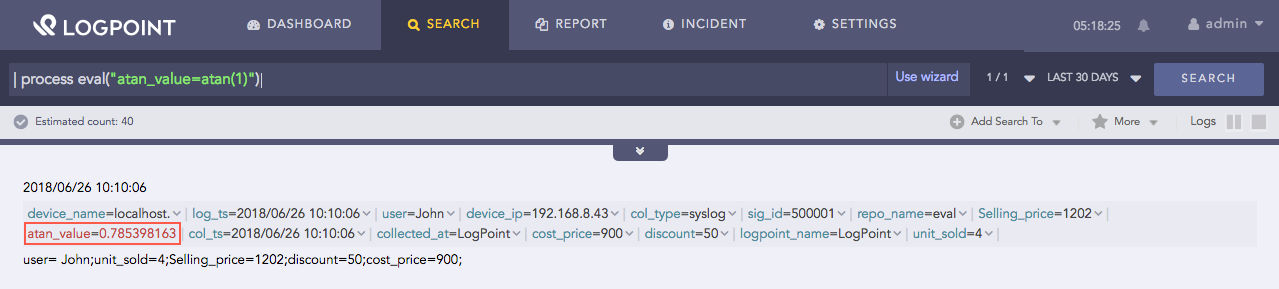
Using atan function¶
Here, the query returns the inverse tangent of 1 in the atan_value identifier.
Accepts one argument X as input and returns the inverse hyperbolic tangent of X.
Syntax:
| process eval("identifier=atan(X)")
Example:
| process eval("atanh_value=atanh(1)")
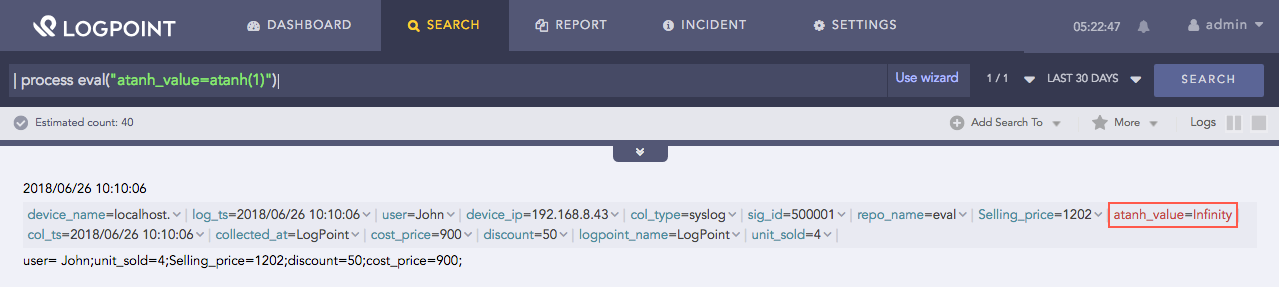
Using atanh function¶
Here, the query returns the inverse hyperbolic tangent of 1 in the atanh_value identifier.
Accepts two arguments X and Y as input and returns the hypotenuse of a right-angled triangle with X length and Y base. It follows the equation of the Pythagorean theorem, (hypotenuse = sqrt{length^2 + base^2}).
Syntax:
| process eval("identifier=hypot(X,Y)")
Example:
| process eval("hyp=hypot(3,4)")
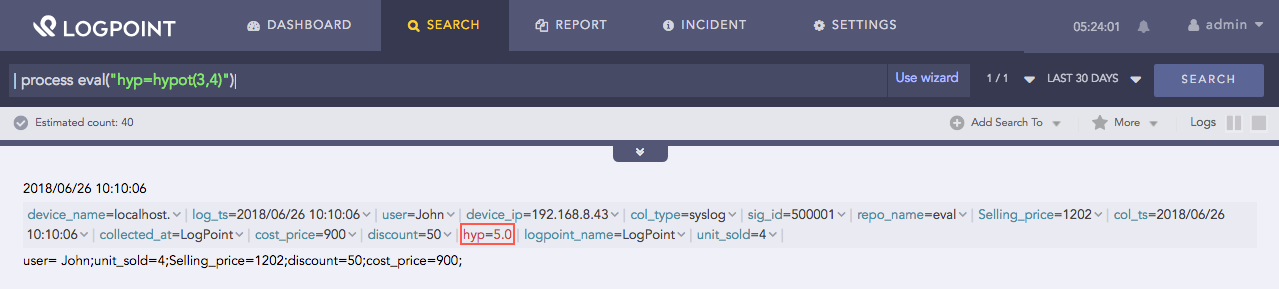
Using hypot function¶
Here, the query calculates the hypotenuse value of the triangle with 3 length and 4 base and returns its value in the tan_value identifier.
We are glad this guide helped.
Please don't include any personal information in your comment
Contact Support